문제
어린 왕자는 소혹성 B-664에서 자신이 사랑하는 한 송이 장미를 위해 살아간다. 어느 날 장미가 위험에 빠지게 된 것을 알게 된 어린 왕자는, 장미를 구하기 위해 은하수를 따라 긴 여행을 하기 시작했다. 하지만 어린 왕자의 우주선은 그렇게 좋지 않아서 행성계 간의 이동을 최대한 피해서 여행해야 한다. 아래의 그림은 어린 왕자가 펼쳐본 은하수 지도의 일부이다.
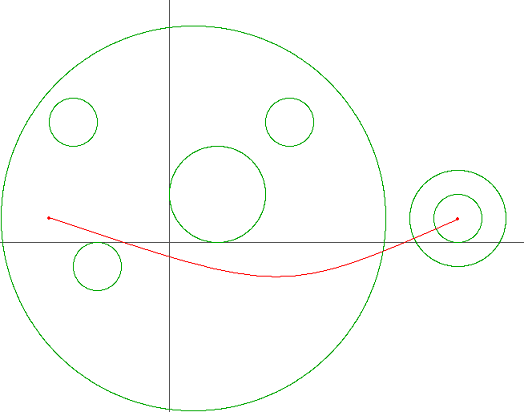
빨간 실선은 어린 왕자가 출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화하는 경로이며, 원은 행성계의 경계를 의미한다. 이러한 경로는 여러 개 존재할 수 있지만 적어도 3번의 행성계 진입/이탈이 필요하다는 것을 알 수 있다.
위와 같은 은하수 지도, 출발점, 도착점이 주어졌을 때 어린 왕자에게 필요한 최소의 행성계 진입/이탈 횟수를 구하는 프로그램을 작성해 보자. 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다. 또한, 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주어지며, 세 번째 줄부터 n줄에 걸쳐 행성계의 중점과 반지름 (cx, cy, r)이 주어진다.
출력
각 테스트 케이스에 대해 어린 왕자가 거쳐야 할 최소의 행성계 진입/이탈 횟수를 출력한다.
제한
- -1000 ≤ x1, y1, x2, y2, cx, cy ≤ 1000
- 1 ≤ r ≤ 1000
- 1 ≤ n ≤ 50
- 좌표와 반지름은 모두 정수
-------------------------------------------------------------------------------------------------------------
풀이
시작점, 도착점 그리고 행성 하나만 존재하는 경우에 대해 생각해보자.
시작점과 도착점이 모두 행성안에 있거나 밖에 있는 경우는 행성계를 통과하지 않는다.
따라서 두 점중 하나가 행성계 안, 다른 한 점은 행성계 밖에 있을 때 행성계를 통과하는 횟수가 하나 증가한다.
행성계의 경계는 결국 원이므로 모든 행성계에 대해서 위 연산을 해주면 된다.
코드
##두 점중 하나만 행성계 내부에 존재할 떄 res + 1
import math
def calc_dist(x,y,c1,c2):
return math.sqrt((x-c1)**2 + (y-c2)**2)
trial = int(input()) #num of test case
for _ in range(trial):
x1, y1, x2, y2 = input().split()
x1, y1, x2, y2 = int(x1), int(y1), int(x2), int(y2)
n = int(input())
cnt = 0
for _ in range(n):
din1, din2 = False, False
c1, c2, r = input().split()
c1, c2, r = int(c1), int(c2), int(r)
d1 = calc_dist(x1,y1,c1,c2)
d2 = calc_dist(x2,y2,c1,c2)
if d1 > r : din1 = True
if d2 > r : din2 = True
cnt = cnt + (din1 ^ din2)
print(cnt)x1,y1은 시작점 x2,y2는 도착점이다.
n은 시험 횟수, n은 원의 개수, cnt는 행성계를 통과하는 수이다.
'공부 > PS' 카테고리의 다른 글
| BOJ 17392: 우울한 방학 (0) | 2022.02.10 |
|---|---|
| BOJ 1003: 피보나치 함수 (0) | 2021.11.07 |
| BOJ 1002: 터렛 (0) | 2021.11.07 |
| BOJ 1001: A-B (0) | 2021.11.07 |
| BOJ 1000: A + B (0) | 2021.11.07 |
